In the previous chapter, we explored different data types and carried out algebraic operations. We created a simple Python program to calculate the area of a circle with the radius as an input. Now, let’s put these concepts into practice by solving another problem – the problem of ages.
| Amita and Madhur are two sisters. The sum of their ages is 43, and difference of their ages is 3. If Amita is the elder sister, what is her age? This is a simple problem of Linear equations, Let Amita’s age be a Let Madhur’s age be b Sum of their ages a+b = 43 eq1 Difference of ages a – b = 3 eq2 eq1 + eq2 —> 2a=46, therefore, a = 46÷2 = 23 b =43 – a = 43 – 23 = 20 we can re-write the solution as a formula a = (eq1 + eq2) ÷ 2 b = eq1 – a |
now, lets create a python program for this: ‘ages.py’
| ages.py |
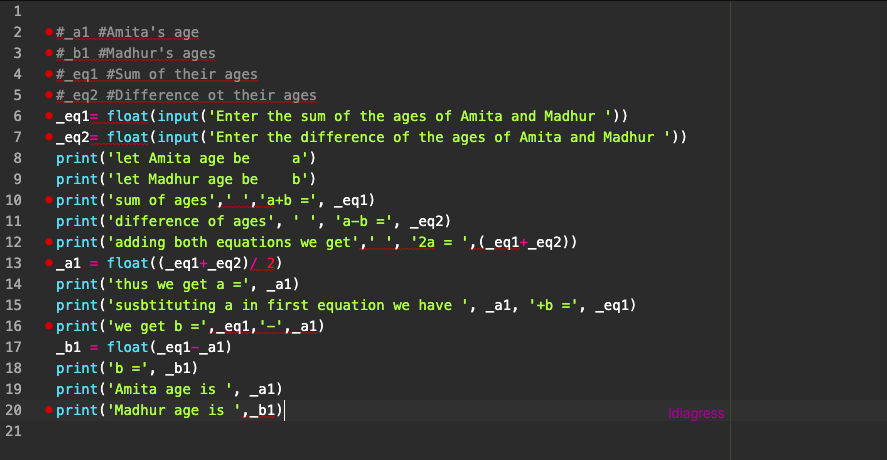
| # _a1 #Amita’s age # _b1 #Madhur’s ages # _eq1 #Sum of their ages # _eq2 #Difference ot their ages _eq1 = float(input(‘Enter the sum of the ages of Amita and Madhur ‘)) _eq2 = float(input(‘Enter the difference of the ages of Amita and Madhur ‘)) _a1 = ((_eq1+_eq2) / 2) _b1 = (_eq1-_a1) print(‘Amita age is ‘, _a1) print(‘Madhur age is ‘, _b1) |
and the output of the above program is,
The variables are _a1, _b1, _eq1, _eq2, virtually by force of habit, I am using underscores in variable names; even if you use straight forward a, b, eq1, eq2 it will be sufficient.
Now, consider a scenario wherein my objectives from the program are changed. I want to make a program whose output is similar to a tutorial for solving the problem, in a stepwise format illustrated above. (ages_with_steps.py)
The answer is the same, only the visual aspect of presenting the output has changed depending on our audience. This is what we had discussed previously as making the code more ‘readable’. As we can see from the output below, we can identify the steps taken in solving the problem
Now, run the program again for a sum of ages as 59, and difference of 5.
Some observations from the output show that to create spaces, we use empty quotes ‘ ’. But, the output is lacking some basics of grammar.
Like instead of ‘Amita’s age is’ we are printing ‘Amita age is.’
The syntax of python is coming in the way of grammar because if we use single quotes in the print command, another intermediate quote will break the string.
In ‘Amita’s age is’ the string will break at Amita, and the rest of the string might go, or we might get an error.
Hence, the print command allows usage of double quotes “ ”.
In double quotes, the single quote will be considered another character, a part of the string.
print("Amita's age is", _a1)
To explore further let us try out an another problem of linear equations.
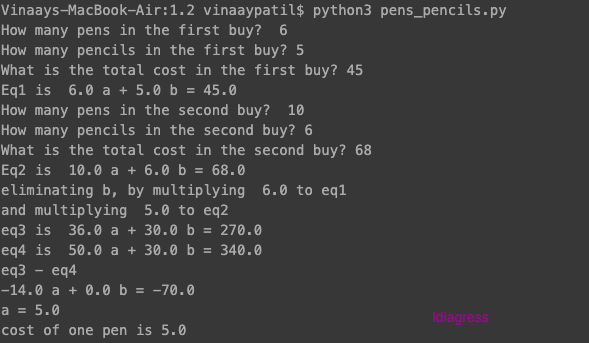
Similar to ages problem, we can convert the solution’s step wise process into a python program — ‘pens_pencils.py‘
Quite a messy program to view; especially line no 24! However, if you check each step, it will correspond to an operation. The program is quite elaborate, detailing every step of the algebraic solution in the output (below)
I have completed the program till you get the value for the pen, as an exercise complete the remainder the program, for calculating the value of pencil.
In the ‘ages‘ problem, we first created a program that captured the essence of the solution. Later, we developed an expanded program that detailed the steps of solving the problem. Now, for the ‘pens and pencils‘ problem, we initially created an expanded program. Let’s work in reverse and create a program that captures the solution’s essence.
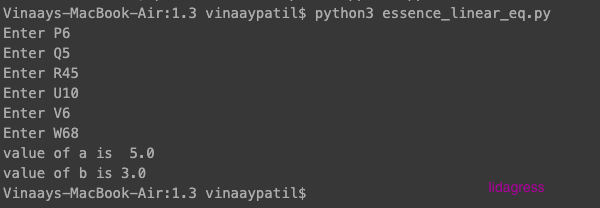
We will now create a python program which will capture this generic version for any linear simultaneous equation:
We’ll name this program ‘essence_linear_eq.py.’ The introduction of intermediate variables, ‘_numerator’ and ‘_denominator,’ not only makes our code cleaner but also helps us track potential mistakes, reducing confusion. This is in contrast to our previous program, where an elaborate ‘print’ command could lead to errors due to a single missing bracket.
print(‘cost of one pen is’,((_p1*_do2)-(_p2*_co2))/((_co1*_do2)-(_do1*_co2)))
The output is as follows
For the generalized program, we can write the logic of our program in a step wise format as below:
| Step No | Step Description | Symbolical Step Presentation |
| 1 | Begin program to solve generic linear simultaneous equations | Pa + Qb = R
Ua + Vb =W |
| 2 | Get Inputs for equation | Get, P, Q, R, U, V and W |
| 3 | Solve for Intermediate variables | Numerator = (R•V) – (W•Q),
Denominator is (P•V) – (Q•U) |
| 4 | Calculate final solution | a=Numerator/Denominator
b = (R – Pa)/Q |
| 5 | Print the final output | Out, a, and b. |
Algorithm
When we create a step-by-step detailing of the program’s logic, it is technically referred to as an ‘algorithm.’ Algorithms serve as a fundamental component of programming, outlining a structured and systematic approach to problem-solving.
Thus our ‘essence_linear_eq.py‘ program captures the core essence or in other words the ‘algorithm’ of solving a problem of simultaneous equations.
Exercise
- Create an algorithm to solve a generic quadratic equation, Ax2 + By + C =0
- Use the algorithm and create a program to find the roots of a quadratic equation, x2 +2x +1 =0. Use hand calculations to verify your answer.
- Use the program created in step 2, to also solve for , x2 +5x +6 =0.
- Find the roots of the equation 2×2 – 5x + 3 = 0
- The product of Jai’s age (in years) two years ago and her age four years from now, is one more than twice her present age. What is her present age? (Jai’s present age — 2) • (Jai’s present age + 4) = 2 * (Jai’s present age) + 1
{Hint, use the quadratic formula for getting the roots, and for finding square root, use the exponential operator, raise to 0.5, (25 ** 0.5 =5)}
Underscore in Variable
Variable names in Python can begin with letters, but using a variable name that matches a built-in Python command or data type can lead to confusion.
For instance, defining a variable as “int = 14” can be problematic because it can get mixed up with the data type ‘int()’ used to declare integers. To avoid such confusion, it’s a good practice to use underscores (‘_’) in variable names. Text editors like Atom often provide better visibility and organization for variables when they start with an underscore.
While all the programs in this chapter could work with integers instead of floats, it’s worth considering the choice of data type based on the specific requirements of the program. In general, using ‘floats’ is recommended when mathematical operations involve division or roots. This is because using integers in such calculations may lead to the truncation of decimal parts, potentially leading to inaccurate results.
For example, if we run the following program:
_a = 32 _b = 5 _c = int(_a/_b) print(_c)
The output we will get is
6
whereas the actual calculation yields 32÷5 = 6.4 the decimal, 0.4 will be ignored in an ‘int’ data type.
Summary
We put our knowledge to practice by solving the “ages” problem, which is a simple case of linear equations. The program ‘ages.py‘ is designed to achieve this. It takes the sum and difference of ages as input and calculates individual ages using the equations.
We also observed that variable names could use underscores (‘_’) for better visibility and organization. However, straightforward names like ‘a’ and ‘b’ would suffice.
To make our output more informative and instructional, we created ‘ages_with_steps.py.’ This program showcases the steps involved in solving the problem, creating a stepwise tutorial-like output for better understanding.
The concept of using double quotes in the ‘print’ command to handle single quotes in strings was introduced. We saw that double quotes allow for more accurate grammar usage.
Then, we explored the “pens and pencils” problem, which also involves solving a system of linear equations. A program, ‘pens_pencils.py,’ was developed to solve this problem, and it provided a detailed output, illustrating each step of the algebraic solution.
Subsequently, we discussed the essence of the solution and its implementation in ‘essence_linear_eq.py.‘ This program captures the core logic of solving generic linear simultaneous equations and presents it in a structured stepwise format. We introduced the concept of an algorithm, which forms the foundation of programming.
In the exercises, you were given challenges related to linear and quadratic equations, encouraging you to use algorithms to find solutions. The importance of variable names and the choice of data types, specifically the preference for ‘floats’ when mathematical operations involve division or roots, was highlighted.
In summary, this chapter expanded our understanding of linear equations, problem-solving techniques, and the use of algorithms. We practiced writing programs to solve real-world problems, making our code more readable, and addressing issues related to variable names and data types. These skills will be valuable as we continue our journey into programming.



















[…] Prev Chapter Course Homepage Next Chapter […]