1.7 User Defined Functions in Python

In our previous example of finding the roots of a quadratic equation using the Bisection Method, we observed that a piece of code was repeated twice: once to calculate the positive root and then again to find the negative root. This repetition involves the same logic with just a change in variables.

# Bisection loop for positive roots while ((_a*_x*_x) + (_b*_x)) != _c and _iter < _limit:     if ((_a*_x*_x) + (_b*_x)) > _c:         _high = _x     else:         _low = _x     _iter = _iter+1     _x = (_high + _low)/2     print(“At”, _iter, ” iteration solution is: “, _x)      print(“After “, _iter, ” iterations the positive root of Equation is: “, _x)

For the negative roots, we repeat the same code with a change in variables:

‘_nhigh‘ replaces ‘_high,’

and

‘_nlow‘ replaces ‘_low.’

# Bisection loop for negative roots while ((_a*_x*_x) + (_b*_x)) != _c and _iter < _limit:     if ((_a*_x*_x) + (_b*_x)) > _c:         _nhigh = _x     else:         _nlow = _x     _iter = _iter+1     _x = (_nhigh + _nlow)/2     print(“At”, _iter, ” iteration solution is: “, _x)      print(“After “, _iter, ” iterations the negative root of Equation is: “, _x) _x)

When a piece of code repeats with only variable values changing, Python offers a powerful feature: User-Defined Functions (UDFs). By defining a UDF at the start of our program, we can call the function anytime within the program to repeat the code. Let’s illustrate this with the same Bisection Loop code.

Defining a User-Defined Function

To define a UDF in Python, you use the def command. You assign a name to the function and declare the variables to be passed into it.

def bisection_loop(_x, _high, _low, _iter=0):

In this function definition, ‘_x,’ ‘_high,’ ‘_low,’ and ‘_iter’ are the variables that change values during execution. ‘_iter’ is assigned a default value of ‘0.’

We can define any ‘names’ for the variables. We can use names like ‘a,’ ‘b’ also. However, to avoid confusion at this early stage, we are sticking to previous variable names. Additionally, we can set the default value for a variable in the function definition itself. We have done this for ‘_iter’ and set the default value to ‘0’. 

We declare the rest of our code below the ‘def’ command.

def bisection_loop(_x, _high, _low, _iter=0):     while ((_a*_x*_x) + (_b*_x)) != _c and _iter < _limit:         if ((_a*_x*_x) + (_b*_x)) > _c:             _high = _x         else:             _low = _x         _iter = _iter+1         _x = (_high + _low)/2         print(“At”, _iter, ” iteration solution is: “, _x)     print(“After “, _iter, ” iterations the positive root of Equation is: “, _x)

Once declared at the start of the program, we can call the function later in the program using the following syntax –

function_name(variable1, variable2, ..., variableN)

In the case of our function, we can call it in the following manner – 

bisection_loop (2, 50, 5 )

Here’s how Python interprets the call:

bisection_loop(_x, _high, _low, _iter=0):   corresponds to bisection_loop(2,50,5)

• _x corresponds to 2
• _high corresponds to 50
• _low corresponds to 5
• _iter gets the default value of 0

Once we understand this correspondence, we can use the same function for calculating the positive and negative roots by merely manipulating the values passed into the function. 

_x = (_high + _low)/2
bisection_loop(_x, _high, _low)
 
_x = (_nhigh + _nlow)/2
bisection_loop(_x, _nhigh, _nlow)

We need to change the value of ‘_x’ before passing it into the function. For the other two values, we already have two different variables in our program. The full program will be as follows – (bisection_function.py)

bisection_function.py

def bisection_loop(_x, _high, _low, _iter=0):     while ((_a*_x*_x) + (_b*_x)) != _c and _iter < _limit:         if ((_a*_x*_x) + (_b*_x)) > _c:             _high = _x         else:             _low = _x         _iter = _iter+1         _x = (_high + _low)/2         print(“At”, _iter, ” iteration solution is: “, _x)     print(“After “, _iter, ” iterations the positive root of Equation is: “, _x)           # program to find roots of the equation # format of equation  Ax2 + Cx = C print(“Enter coefficients in the format Ax2 + Bx = C”)   _a = float(input(“Enter the coefficient of x2  : “)) _b = float(input(“Enter the coefficient of x   : “)) _c = float(input(“Enter the coefficient on RHS : “))   # Define interval _low = float(input(“Enter the lower interval for solution  :”)) _high = float(input(“Enter the higher interval for solution :”))   # Negative interval _nlow = -(_low) _nhigh = -(_high)   # Define iteration _limit _limit = int(input(“Enter the iteration limit for solution :”))_x = (_high + _low)/2 bisection_loop(_x, _high, _low)   _x = (_nhigh + _nlow)/2 bisection_loop(_x, _nhigh, _nlow)

We get a much crisper code by using the function, now let us see if it works

We can make a few improvements to the code :

1. Firstly, since we are passing values, no need to have separate variables ‘_nhigh’ and ‘_nlow’. We can pass negative values of ‘_high’ and ‘_low directly into the function

bisection_loop(_x, _high, _low)

bisection_loop(_x, -(_high), -(_low))

2. Secondly, we can insert the calculation for ‘_x’ within the function. 

Implementing our improvements, we get a condensed code. 

The output for our improved program is as follows

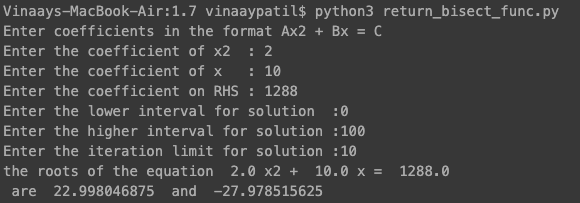
The output is the same as the previous programs. 

Upon running our program with the user-defined function, you might notice an unexpected output. Specifically, the last line of the print statement for the negative root, ‘–27.97’, mentions, “After 10 iterations, the positive root of Equation is: –29.97.” Why does this happen?

The issue arises because the variable ‘_x’ is declared within our function, and the ‘print’ command falls outside the function scope. To resolve this and improve the clarity of our code, we can include an ‘if…else’ branching to check for the sign of the root.

However, this approach can make our code look somewhat clumsy. Moreover, another problem remains: we are not storing the roots. In each execution of the function, ‘_x’ is overwritten, preventing us from retaining both the positive and negative roots for further use.

---

 Return option in Python Functions

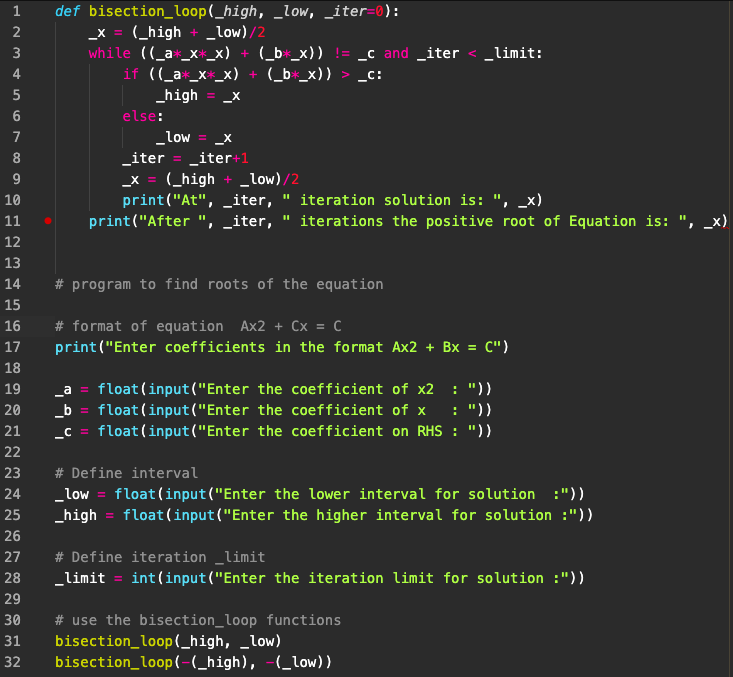
To resolve both issues—correcting the output discrepancy and storing the roots—Python functions provide a handy feature known as ‘return.’ This feature allows us to obtain a value from the function. In our case, we aim to return the value of ‘_x.’

Here’s how we can incorporate the ‘return’ statement at the end of our ‘bisection_loop’ function:

bisection_loop(_high, _low, _iter=0):     _x = (_high + _low)/2     while ((_a*_x*_x) + (_b*_x)) != _c and _iter < _limit:         if ((_a*_x*_x) + (_b*_x)) > _c:             _high = _x         else:             _low = _x         _iter = _iter+1         _x = (_high + _low)/2     return _x

We can then store the returned value into another variable as follows –

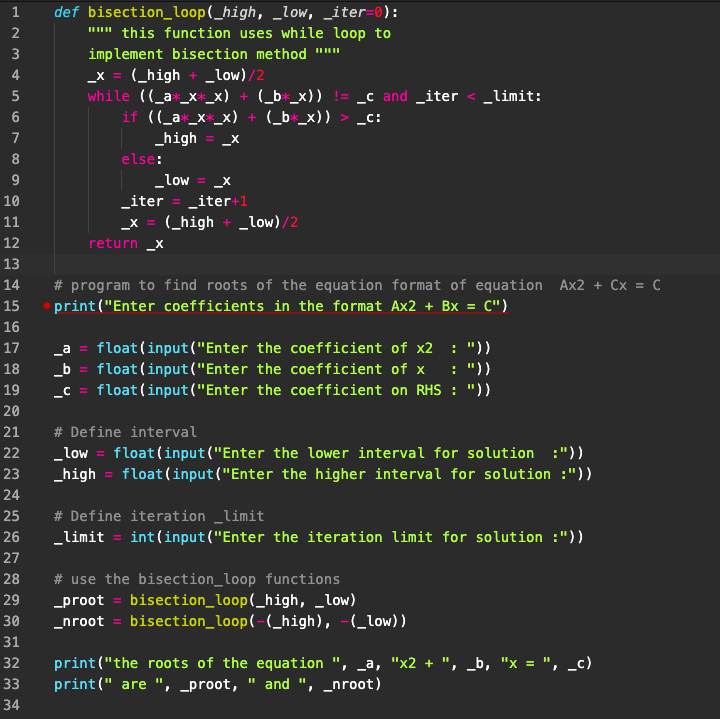
_proot = bisection_loop(_high, _low)
_nroot = bisection_loop(-(_high), -(_low))
  

‘_proot’ will store the ‘returned’ value of ‘_x’ from bisection_loop(_high, _low)

Similarly we will store the value in ‘_nroot’ ( Important : We can return only one value from the function)

It’s crucial to note that a function can return only one value. This usage of the ‘return’ feature enhances the clarity and functionality of our code, allowing us to easily manage and utilize the roots. Moreover, the triple double-inverted commands within the function definition act as comments, making the code more readable and self-explanatory

The Bisection loop program with ‘return’ statement is as follows

The triple double-inverted commands within the function definition act as comments. These comments make the code more ‘readable’.

The output is as follows

Summary

• Roots of Quadratic Equation:
  • Applied bisection to find the roots of a quadratic equation, providing an example using Python.
  • Explored the challenges of determining the solution interval and dealing with both positive and negative roots.
• Creating User Defined Functions:
  • Introduced User Defined Functions (UDFs) to avoid repetitive code.
  • Demonstrated how to define a UDF using the ‘def’ statement and return values from it.
  • Utilized UDFs to simplify the code for finding the roots of the quadratic equation.
• Improving Code with ‘Return’ Statements:
  • Explained the usage of the ‘return’ statement to retrieve values from a function.
  • Showcased how ‘return’ can enhance code readability and store results for further use.

---

Prev Chapter   Course Homepage    Next Chapter